New Publication: Shape matters: cell geometry determines phytoplankton diversity

We just posted a new study on bioRxive in which we study the shape-diversity relationship in unicellular phytoplankton.

Background

One of the big questions of modern biodiversity research revolves around the relation between taxonomic richness and morphological traits, that is the question, which biological characteristics are prone to strong ecological diversification. Often body size is taken as a master trait for many other characteristics and indeed it was found that species richness of certain taxonomic groups (e.g., insects or mammals) exhibits a unimodal dependency on body size. In this study we go one step further and show that body shape (the geometric form of an organism) could play an equally important role - at least for unicellular marine phytoplankton.

Phytoplankton constitute the major group of aquatic primary producers, they form the base of all marine food webs and are of vital importance to the functioning of the whole marine ecosystem. Marine unicellular phytoplankton are also notorious for their enormous morphological diversity, with cell volumes spanning many orders of magnitude and dozens of different shape types, from simple spherical to extremely complex geometries. This huge variety in phytoplankton cell volumes and shapes presents a unique opportunity for investigating the influence of organism shape as a driver for larger-scale ecological patterns.

Starting off: relations between cell size and volume

The driving force behind this study is Alex Ryabov, a member of my research group on mathematical modelling. The project initially began as a follow-up on our recent paper on length-volume relationships in lake phytoplankton. But it really gained momentum when Alex got hands on a novel dataset on unicellular phytoplankton data from different oceans and we, together with our other co-authors, started to explore the relationship between cell size and volume. We wanted to test whether shape systematically varies with body size, e.g. bigger cells appearing more as needles. Several studies had argued that such an elongation should be beneficial for the volume-specific nutrient uptake and therefore had hypothesized that large cells should be elongated to increase the surface to volume ratio. Our analysis shows that this is not the case. We found that cell dimensions scale on average with volume isometrically (technically we found that cell surface area increases with cell volume approximately as a power-law with exponent 2/3, over a range of cell volumes spanning 8 orders of magnitude) - meaning there is no evidence for shape elongation with increasing size.

Quantifying cell geometries and cell elongation

The project may have stopped at this point if Alex had not noticed an inconspicuous broadening of data points on our size-volume plot in the range of intermediate cell sizes. Seemingly something was going on there. Luckily, the data base contained information not only on cell sizes but also on cell geometries, that is, whether cells were spheres, cylinders, cones, prisms, or something else out of 38 fundamental shape type. To make use of this, Alex went through the tedious process of calculating for each of these shape types an analytic formula for determining cell volume and cell surface from the measured cell linear dimensions. On a side remark, this not only resulted in the currently most comprehensive compilation of such formula for calculating cell shapes, but also let to the discovery of several errors in existing smaller lists from the literature.

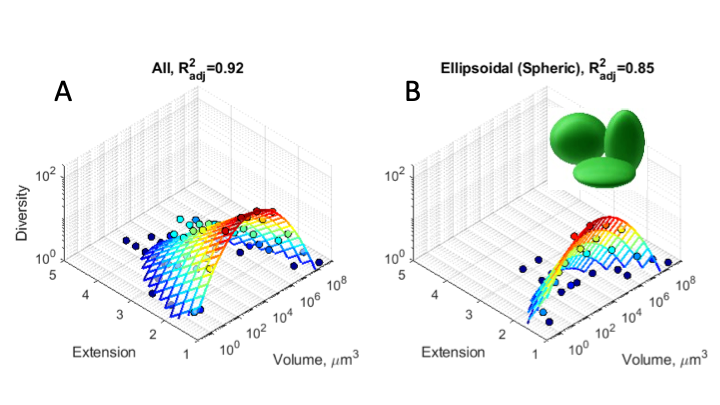
Based on this we were able to determine cell elongations for all phytoplankton cells in the data base. Thereby, we quantified cell elongation either as the aspect ratio of maximal to minimal linear dimensions or as the relative surface area extension, i.e., the gain in cell surface area relative to a spherical cell of the same volume. The surprising result was a hump-shaped dependency of cell elongation on cell volume: Cells of intermediate volume exhibit the greatest shape variation with shapes ranging from oblate to extremely elongated forms, while very small and large cells are mostly compact (e.g., spherical or cubic).

Using cell shape as a predictor of taxonomic richness

Next, we asked whether these findings would translate to the level of biodiversity patterns. This was confirmed in our data analysis, revealing cell shape as an important driver of taxonomic diversity, comparable in magnitude to the effect of cell volume. In total, cell volume and cell elongation taken together allow a remarkably good prediction of global taxonomic richness of marine phytoplankton, explaining 92% of the variation in phytoplankton diversity. We show that taxonomic richness decays exponentially with cell elongation and displays a log-normal dependency on cell volume, peaking for compact cells of intermediate volume.

The results were robust over different phytoplankton phyla and were obtained across different trophic guilds (autotrophs, mixotrophs, and heterotrophs). However maximal cell elongations were reached only in autotrophs (with maximal aspect ratio up to 100), whereas maximal aspect ratios in heterotrophs and mixotrophs was about 10, likely because these two groups need to swim actively.

Implications: evolutionary constraints on cell morphology

Our results have far reaching implications. It is well known that organisms’ size and shape have a profound influence on ecophysiological performance and evolutionary fitness. This holds true also for phytoplankton, where the cell geometry is known to affect most aspects of phytoplankton survival, from grazing by zooplankton to sinking and diffusion, diffusive transport limitation and nutrient uptake. Our findings therefore help us to unravel the ecological and evolutionary constraints on phytoplankton diversity in the ocean.

We have recently posted our findings to BioRxive and submitted to peer review process. We will be very interested to find out what our reviewers have to say to this study.

Update (May 2021): In the meanwhile the study has been published in Ecology Letters