Story behind the paper: Optimal stock-enhancement of a spatially distributed renewable resource
We recently published a study on optimal control in spatially extended ecosystems. Here's the story behind the paper.
Background - optimal control and pattern formation theory
We are all aware of the multiple threats facing ecological systems and wildlife on our planet, related to global climate change and the ongoing decline of natural habitats and biodiversity. In view of these challenges, it becomes an increasingly important task to find means for an optimal management of these systems. Yet, identifying the best control measures turns out to be a challenging task because it typically involves finding a compromise between different (typically, monetary and environmental) requirements, while any intervention entails non-linear effects on the immediate and future states of the system.
These challenges take on a new dimension in spatially extended systems, because control measures have to be chosen not only for any time instance, but also at every point in space. This raises the question of how management activities should be optimally distributed in space. Specifically, is it beneficial to spread the control measures as much as possible, while allocating an equal share of management effort to every location? Or, could there be situations where an alternative policy is best, focusing efforts to a few selected locations at the cost of neglecting other areas? The answer to these questions is not only of theoretical interest but also has immediate practical consequences, for example, for the optimal design of nature reserves and restoration areas.
In German, we would call the first policy “Gießkannenprinzip” (watering can principle), which basically describes the principle of giving everyone an equal share of something. Watering cans often have many holes in the cap where the water pours out, allowing uniform distribution of water on the plants in a bed. The “watering can principle” therefore describes a policy where control efforts are distributed equally among locations.

The watering can principle seems to be a natural strategy. Would then not any deviation from this principle defy our natural intuition? At first glance yes, in an otherwise homogeneous system most people would also expect a homogeneous distribution of control measures to be most effective. But, as it turns out, this is not always the case. A first hint why heterogeneously distributed control efforts potentially can be beneficial stems from pattern formation theory.
Pattern formation describes a counter-intuitive phenomenon in reaction-diffusion systems, where spatially uniform solutions can unexpectedly become unstable, so that concentration profiles evolve towards solutions with localized and patterned states. While pattern formation might go against the intuitive expectation, it is a frequently observed phenomenon in natural and ecological systems (see this text book for a nice review).
In this sense, our study is actually about connecting optimal control to pattern formation theory and we can phrase our central question as follows: Can we apply pattern formation theory to understand under which circumstances a watering can principle is not optimal for the management of spatial and distributed systems?
What was already known - optimal control theory and fisheries
A mathematical rigorous framework for identifying the best possible management of a system for a period of time is provided by optimal control theory. It applies if the model equations and constraints of a system are analytically known. Then, the optimal path of a control variable can be derived by Pontryagin's maximum principle. This principle can be regarded as an extension of the well-know method of Lagrange multipliers which allows finding optimal solutions to a problem with constraints. In an optimal control problem, the constraints are posed by the model equations, so that the Lagrange multiplier (in this context denoted as co-state or shadow prize) becomes a function of time and can be systematically determined by solving a Hamiltonian system (the so-called canonical system). Despite the success of optimal control theory, proven in numerous applications in engineering, operation research, and ecology, not so much is known about optimal control in spatial systems.
To date, most applications of optimal control theory in spatially extended ecosystems have been devoted to optimal fishery and the design of marine reserves. In a seminal modelling study, Neubert (2003) found that a spatially heterogeneous distribution of fishing efforts can be optimal. If fishing rates are reduced in designated no-take areas, the total yield, averaged over the whole range of the spatial system, is maximized. Thus, Neubert (2003) concluded that the establishment of no-take reserves should always be part of an optimal harvest strategy. This heterogenous harvesting solution, however, does not originate from a genuine pattern formation process. Instead, the patterns are directly imposed by the conditions at the boundaries of the domain, where fish stocks were set equal to zero. This type of hostile boundary conditions negates the homogeneity of the spatial domain and therefore it should not come as a surprise to obtain spatial heterogenous solutions. Furthermore, in such as situation the advantage of heterogeneous control measures is only gained close to the boundary, so that with increasing system size the relative merit of heterogeneous control vanishes.
From a theoretical perspective, a more natural assumption is to impose no-flux boundary conditions. This models a situation where stocks can live at, but cannot transgress, the boundary of the habitat, and thus captures situations where natural (e.g., shores) or man-made barriers (e.g., highways) constitute impenetrable boundaries. In this case, spatially homogeneous solutions are compatible with the model — and the question of whether or not spatially patterned solutions are optimal becomes meaningful and significant.
The emergence of heterogeneous optimal management strategies in a truly homogeneous spatial domain was first observed and mathematically investigated by Brock and Xepapadeas (2008). Subsequently, other authors extended that work and showed that similar patterned optimal strategies emerge in population models with two species or when the control actions generate an externality, for example when fishing damages the habitat. However, little was known about whether patterned optimal control solutions emerge also in the absence of externalities and in different model classes. Furthermore, it was an open questions how one should dynamically control a system towards its optimal steady state given some initial spatial configuration.
Building a team and setting-up the stock-enhancement model
This was the problem area where we wanted to make a contribution. I teamed-up with Hannes Uecker from the Institute for Mathematics in Oldenburg, who actually introduced me to this interesting question. Our plan was to join his broad experience on partial differential equations and pattern formation with mine on theoretical ecology. Around 2017 an opportunity came up with the just funded Helmholtz Institute for Functional Marine Biodiversity HIFMB. As I am a founding member of this institute, I got the chance to dedicate one position in the HIFMB postdoc pool with this topic. We were lucky to attract Thorsten Upmann for this position. Thorsten is an expert in economic modelling and control theory, and so we had gathered a sufficiently broad range of expertise to tackle this problem. Later on, our small team was still strengthened by Liv Hammann who used this topic as the subject of her master's thesis project.
Our first goal was to find out whether pattern formation in an optimal control problem can also arise in other ecological model classes. Thus, we deliberately chose the most generic population model, the logistic growth of a single-species population, our stock, which we interpreted as a spatially distributed renewable resource. Would such a simple conceptual model setting be sufficiently rich to admit patterned optimal steady states?
In contrast to a standard optimal harvesting problem, where the resource is reaped to maximize the discounted profit, we designed a set-up where the agent or policy maker has little or no interest in consuming the stock. Instead, either because of ecological concerns or because of economic incentives, the agent is interested in the conservation of the resource and is able to foster its growth and prosperity by means of some costly, spatially targeted stock–enhancement activity such as cultivation, breeding, fertilizing, or nourishment. To make stock-enhancement necessary, we added an overall mortality term into our population model, so that without support by the agent the stock would go extinct. Our question then was, how such stock-enhancement activities should be distributed optimally in time and space in order to maximize total resource abundance and minimize total management costs?
Our main finding: patterned optimal stock-enhancement solutions
Numerically this is not an easy problem to address.
In a spatial system, the canonical equations turn into partial differential equations and, what makes things especially difficult, in the equations of the costates suddenly terms with negative values of the diffusion constant appear. Such systems are inherently unstable and indeed the canonical steady state turns out to be a saddle-point. Thus, numerically one needs to adjust the initial values of the costates along the stable manifold of the saddle point, so that that the system is attracted towards the so-called canonical steady state.
To achieve this numerically, we used the continuation and bifurcation tool
pdepath
from Hannes, which allowed us to compute an overview of the steady states of the canonical system, as well as their stability and spatial structure.
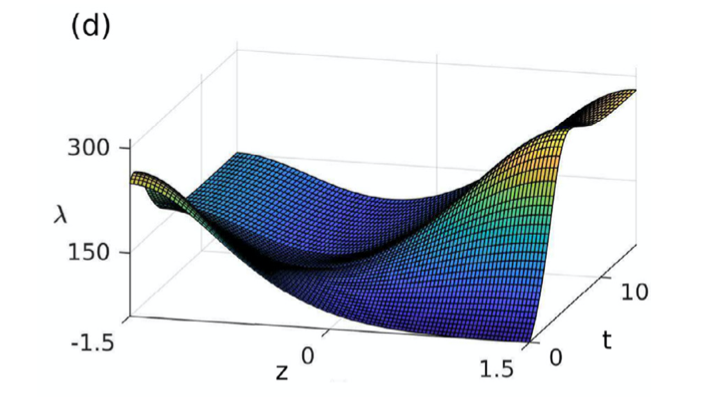
Our simulations showed that indeed patterned optimal solutions emerge in very different geometries, both in discretely coupled habitat patches and in spatially continuous one-dimensional and two-dimensional domains. In the resulting patterned optimal steady state, the agent finds it optimal to concentrate the stock-enhancement activity on some locations, and to curtail it on the rest of the region. Intuitively, the observation that spatially focused efforts may be optimal, can be explained by the fact that locally elevated growth rates in controlled locations generate source–sink dynamics, which helps stocks to recover in non-controlled locations. Thus, the same total stock abundance can be maintained with a smaller investment of management efforts. Interestingly, we found that spatially heterogeneous controls are optimal only if the stock mortality rate is above a critical threshold, that is, exactly in those situations in which the system is under strongest stress it profits most from heterogeneous management.
Multiple steady states and canonical paths
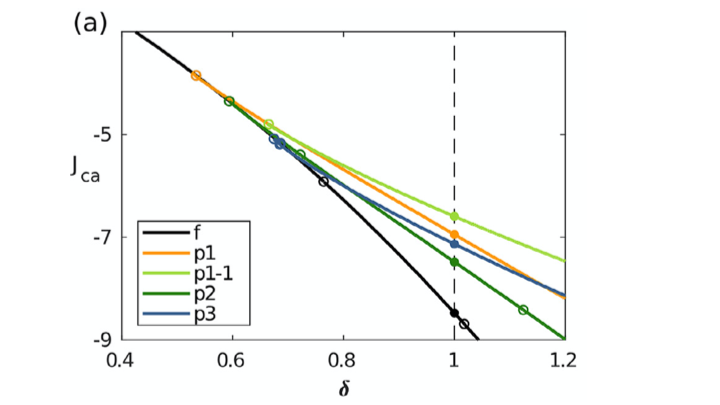
The analysis is further complicated by the fact that in the interesting parameter range, our spatial model exhibits multiple, homogeneous and heterogeneous, steady states, many of which are not stable; while even in systems that exhibit locally stable patterned control states, these are not necessarily optimal.
Thus, our task was to compute the global bifurcation structure and the optimal time-dependent paths to govern the system from some initial spatial configuration to a specified target steady state. Our finding that such optimal paths indeed can be found is ecologically fundamental because these paths describe how to govern the system optimally to the specified steady state. We were thus able to model the policies to be followed during a transition period, a period that may last for quite a long time and may thus, from a management perspective, be quite important.
Limitations and outlook
Even though we were successful to demonstrate the power of sptial optimal control in a generic ecological model, many questions remain open. For example, the question of robustness to external disturbances and noise is still unresolved. What is more, it is totally unclear how one should manage intrinsically heterogeneous systems where certain locations are a priori distinguished from the rest of the system. Should patterned management focus on such intrinsically benign locations or, on the contrary, on those with poor conditions?
But the most unsatisfactory aspect for me personally is that the we still have not developed approaches that allow us to gain a real intuitive understanding of spatial optimal control. Right now, for every new model candidate there is nothing left for us to do but to go through the whole technical machinery of Pontryagin theory, numerically solve the corresponding canonical system, compute the resulting states and optimal paths - and to accept whatever comes out as the optimal strategy. Whereas, if we truly had what I would call a satisfying theory of spatial optimal control, we should be able to guess at the spatial structure of the optimal states just from inspection of the structural properties of the model equations alone, without such a complicated and technical computation procedure. In this sense, I am looking forward to future research to make this breakthrough.
In the meantime, I hope that we were able to make a contribution that is not negligible. This was an exciting project and, most of all, I learned a lot about optimal control.