COVID-19: Biogeography
Here, I analyse the biogeography of the COVID-19 pandemie in different countries. Data are based on the Johns Hopkins repository.
New publication: Power-law distribution in the number of confirmed COVID-19 cases
Me study on macroepidemiological patterns of COVID-19 outbreak just appeared in (Chaos 2020) (see also the free version on Arxiv).
Power-law distribution in confirmed COVID-19 cases in countries worldwide
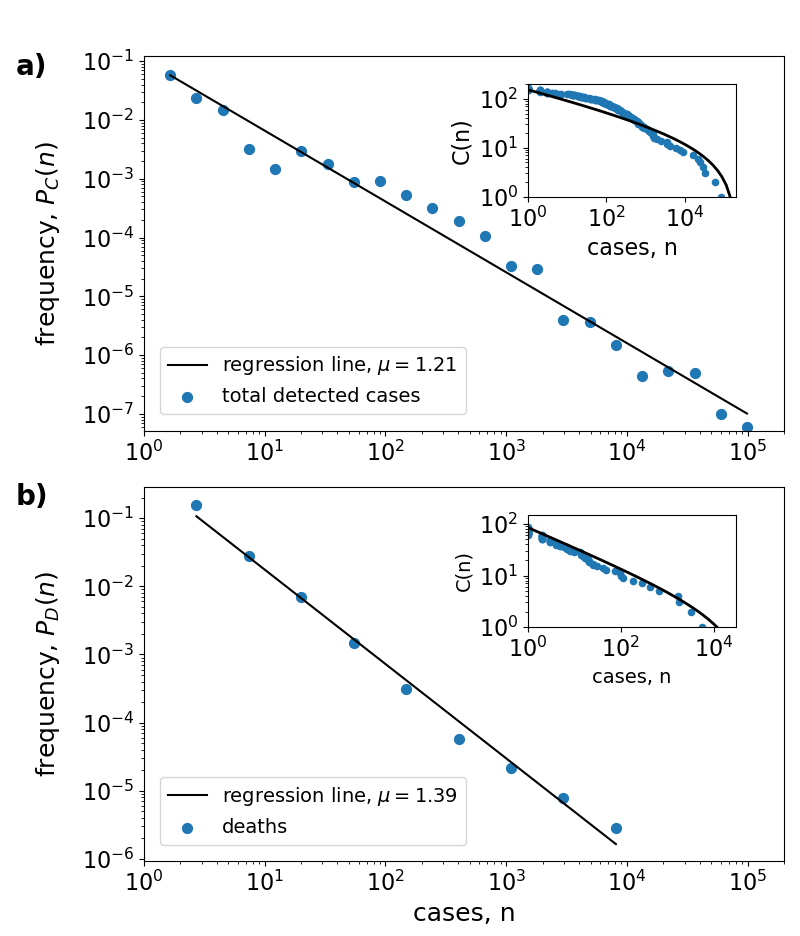
Fig.1: Power-law scaling in the country-level distribution of COVID-19 cases.
The figures show the estimated probability $P_x(n)$ for a country to have a certain number $n$ of
a) confirmed cases (x=C) and
b) confirmed deaths (x=D) on 22 March, 2020.
Histogram bins are spaced equally on a logarithmic axis
and only bins with a positive number of entries are shown.
Black solid lines show straight-line fits with slope $\mu$, indicated in the figure labels.
Insets: Cumulative number $C(n) =\sum_{m=n+1}^N P(m)$ of countries with
case number $m > n$.
Solid lines show the cumulative distribution $C(n) = n^{1-\mu}- n_f^{1-\mu}$
of a truncated power law with cut-off value
a) $n_f=2 \cdot 10^5$ and
b) $n_f=5 \cdot 10^4$.
Power-law distribution in confirmed COVID-19 cases in counties in the US
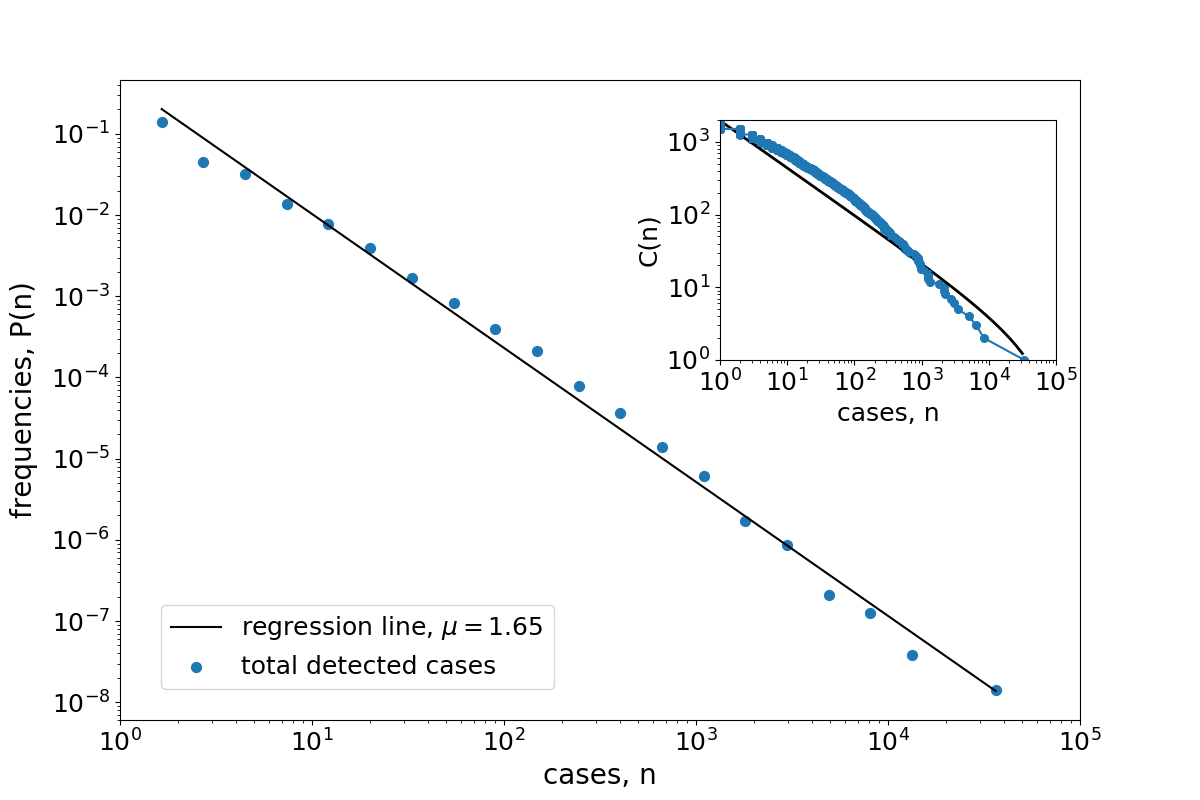
Power-law scaling in the distribution of confirmed COVID-19 cases
in the 1962 US counties that have been invaded by the coronavirus on March 29, 2020.
Details as in Fig.1a.
The cut-off value for the cumulative distribution in the inset was set to $n_f=1\cdot 10^5$.
Coronavirus arrival times
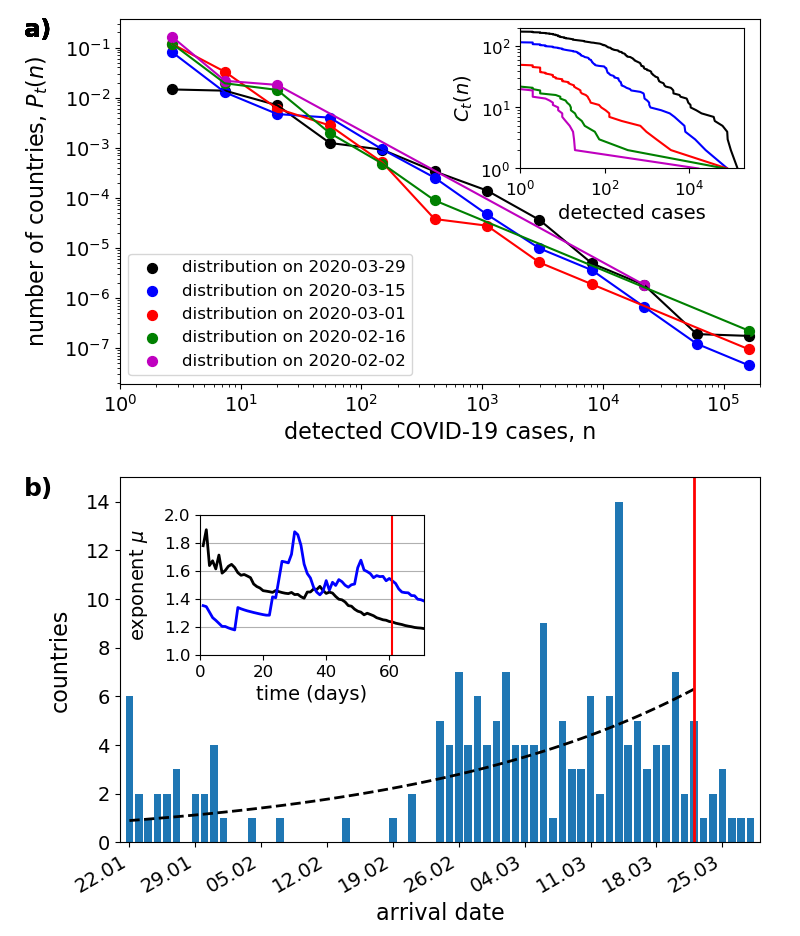
Fig.3:
Temporal development of the COVID-19 pandemic.
a) Evolution of the distribution of confirmed cases per country.
The same as Fig.1a, but for five different time instances separated by 2 weeks (see figure legend)
during the pandemic.
b) Distribution of arrival times.
The histogram shows the number of countries that were invaded by the virus
on a certain day between Jan 22, 2020 and March 29, 2020 (blue bars).
Further shown is an exponential increasing function, $\exp(s t)$ (black dashed line) with growth rate
$s=0.03 \ d^{-1}$, obtained by a least square fit to the histogram during the first 61 days.
The inset shows the critical exponents $\hat{\mu}_C(t)$ (black) and $\hat{\mu}_D(t)$ (blue)
as a function of time. The vertical red line indicates 22 March.