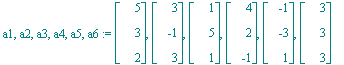
Eine Bearbeitung der   Aufgabe (16)  mit Maple.

Wenn Sie Zugang zu einer Maple-Version ab 9.5 haben - z.B. ueber die Ihnen am Standort Wechloy zugaenglichen Rechner - dann können Sie hier meine mws-Datei runterladen.

>

restart:

>	with(LinearAlgebra):with(plots):

Warning, the name changecoords has been redefined

Die gegebenen Punkte sind:

>	a1,a2,a3,a4,a5,a6:=<5,3,2>,<3,-1,3>,<1,5,1>,<4,2,-1>,<-1,-3,1>,<3,3,3>;

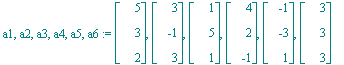
Zusammengefasst zu einer Matrix:

>	A6:=Matrix([seq(a||k,k=1..6)]);

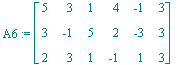
Der zu betrachtende Punkt ist:

>	beta:=1/6*<1,1,1,1,1,1>:x:=Multiply(A6,beta);

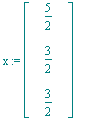
Man kann sich das wie folgt ansehen und drehen mit der Maus:

>	P1:=pointplot3d({seq(a||k,k=1..6)},axes=BOXED,symbol=box, symbolsize=20,axes=boxed,labels=[xx,yy,zz],color=red):

>	P2:=pointplot3d({x},axes=BOXED,symbol=box,symbolsize=20,axes=normal,labels=[xx,yy,zz],color=blue):

>	display(P1,P2);

Nun zur Lösung der Aufgabe:

Gesucht  ist eine Linearkombination der a1,...,a6, die 0 ergibt und mit Koeffizientensumme 0. Siehe Beweis des Satzes von Radon.

>	A61:=<A6,<1|1|1|1|1|1>>;

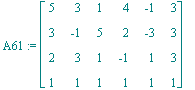
>	sols:=LinearSolve(A61,<0,0,0,0>,free=s);

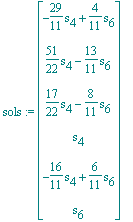
Wähle nun willkürlich (Strategie ?) eine Lösung

>	alpha:=map(u->subs(s[4]=0,s[6]=11,u),sols);

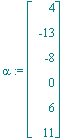
Normierung, so dass die Summe der positiven Einträge 1 ergibt:

>	alpha:=1/21*alpha;

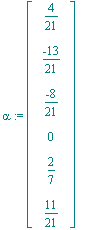
Nun folge ich dem Beweis des Satzes von Caratheodory. Die   sind hier entsprechend der Aufagbenstellung alle  .

Das Minimum der   ist hier  .

Dann wird gesetzt

>	g6:=Add(beta,alpha,1,-21/11/6);

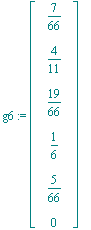
Nun wird durch Nachrechnen bestätigt, dass der gegebene Punkt   auch durch folgende Kombination dargestellt werden kann:

>	Multiply(A6,g6);

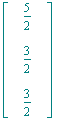
Nun ist das Gleiche mit den 5 verbleibenden Punkten a1,...,a5 zu machen. Dabei ist jetzt

>	L:=[]: for k to 6 do if not g6[k]=0 then L:=[op(L),k]; fi;od; if nops(L)<5 then print(`Vorsicht: mehr als ein Eintrag 0`);fi; #print(L):

>	beta||5:=g6[L];

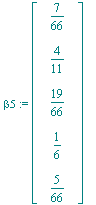
>	A5:=A6[1..3,L];

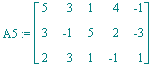
>	A51:=<A5,<1|1|1|1|1>>;

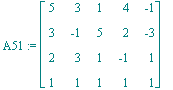
>	sols5:=LinearSolve(A51,<0,0,0,0>,free=s);

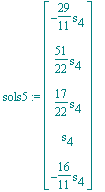
wähle willkürlich (Strategie ?) eine Lösung

>	alpha||5:=map(u->subs(s[4]=22,u),sols5);

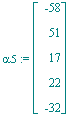
Normierung, so dass die Summe der positiven Einträge 1 ergibt:

>	r:=0: for k to 5 do if alpha||5[k]<0 then r:=r+alpha||5[k]; fi;od:

>	alpha5:=Multiply(1/r,alpha||5);

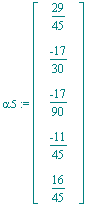
Das Minimum der   ist hier  :

>	seq(beta||5[k]/alpha||5[k],k=1..5);

>	m:=add(abs(beta||5[k]/alpha||5[k]),k=1..5):

>	for k to 5 do if beta||5[k]/alpha||5[k]>0 and beta||5[k]/alpha||5[k]<m then m:=beta||5[k]/alpha||5[k];fi;od;m;

Dann wird gesetzt

>	g5:=Add(beta||5,(-m)*alpha5);

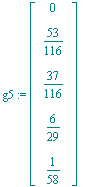
>	Multiply(A5,g5);

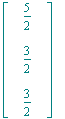
Die Frage ob es mit weniger als vier Vektoren geht bleibt offen. Dies kann allerdings nur dann eintreten, wenn der Punkt x zusammen auf einer Grade oder Ebene liegt, die von zweien oder dreien der a1,..., a6 aufgespannt wird.

Eine alternative Lösung der Aufgabe  wäre:

Durch eine Skizze geeignete Punkte erraten. Obiger Punktgraph legte mir z.B. dann nahe, es mit den Punkten     zu versuchen. Das klappte dann aber nicht.

Natürlich kann man Maple auch einfach suchen lassen, um alle Möglichkeiten zu finden:

>	M:={1,2,3,4,5,6}:

>	for i to 5 do

>	for j from i+1 to 6 do

>	MM:=convert(M minus {i,j},list);

>	for k to 4 do n:=MM[k];b||k:=a||n;od;

>	Ax:=<b1|b2|b3|b4>;

>	Ax1:=<Ax,<1|1|1|1>>;

>	solx:=LinearSolve(Ax1,<x,1>,free=sx);

>	if not solx[1,1]<0 and not solx[2,1]<0 and not solx[3,1]<0 and not solx[4,1]<0 then print(Spaltenauswahl=MM,Koeffizientenvektor=solx,`Summe der Koeffizienten`=add(solx[k,1],k=1..4),`Probe:  Spaltenauswahlmatrix*Koeffizientenvektor`= Multiply(Ax,solx));fi;

>

od;

>

od:

Man sieht, es klappt sogar mehrfach!

>