zu Aufgabe (29)
(a)
Vorbereitungen:
| > | restart: |
| > | with(LinearAlgebra): |
| > | u,v,w,x:=<1,2,3>,<2,3,1>,<3,1,2>,<1,1,1>; |
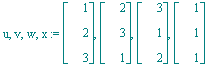
Die vier Vektoren sind affin unabhängig:
| > | for y in [u,v,w,x] do <u-y|v-y|w-y|x-y>,Rank(<u-y|v-y|w-y|x-y>);od; |
Nach Satz 7 in § 1 genügt eine der 4 Rechnungen!
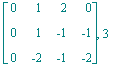
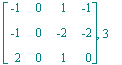
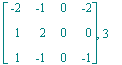
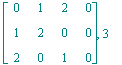
Lösungsidee:
Bestimme die beiden projektiven Schnittpunkte "gegenüber liegender Seitenpaare" des "Vierecks".
Diese spannen eine (projektive) Grade G auf, der zugehörige Untervektorraum U dient dann als "unendlich ferne Hyperebene". mit einem Vektor s aus
![]() \
\
![]() erfüllt dann
erfüllt dann
![]() die Anforderungen der Aufgabenstellung.
die Anforderungen der Aufgabenstellung.
Nun zur Ausführung:
Die Wahl der Seitenpaare ist allerdings nicht eindeutig.
Bis auf Anordnung gibt es zunächst drei Möglichkeiten, gegenüberliegende Seiten festzulegen: {a,b} und {c,d}, {a,c} und {b,d}, {a,d} und {b,c}.
Zu jeder solchen Paarung gibt es zwei Möglichkeiten, die beiden weiteren "Viereckseiten" festzulegen.
Bei genauerem Hinsehen stellt man fest, dass es bis auf Anordnung nur drei Möglichkeiten gibt, die vier Seiten zu wählen und in Paare zu gruppieren:
{a,b} und {c,d}, {a,c} und {b,d}
{a,b} und {c,d}, {a,d} und {b,c}
{a,c} und {b,d}, {a,d} und {b,c}
Für den Aufgabenteil (a) genügt es, für eine der Konstellationen eine geeignete Hyperebene anzugeben, und damit die gestellte Frage positiv zu beantworten.
Im Folgenden geschieht dies für die Seitenpaare {a,b} und {c,d}, {a,d} und {b,c}.
Bestimmung von G bzw. U:
Erzeugende Vektoren für die gesuchten projektiven Schnittpunkte sind:
| > | S1:=op(IntersectionBasis([[u,v],[w,x]])); |
| > | S2:=op(IntersectionBasis([[u,x],[v,w]])); |
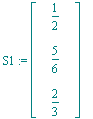
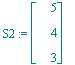
Die Spalten der folgenden Matrix MU erzeugen U:
| > | MU:=<S1|S2>; |
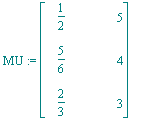
Auch die Wahl des Stützvektors v ist nicht eindeutig.
Man könnte ihn z.B. auch senkrecht zu
![]() wählen:
wählen:
| > | s:='s':s=13*NullSpace(Transpose(MU))[1]; |
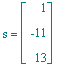
Ich wähle
| > | s:=<1,0,0>; |
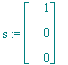
Betrachtet wird nun die Hyperebene
![]()
Bestimmung der Schnittpunkte aH , bH , cH , dH der projektiven Punkte mit H.
Gesucht sind also geeignete Streckungsfaktoren (Strf) für die Erzeuger der projektiven Punkte a,b,c,d.
Etwa für a erhält man diesen Faktor so:
Es muss gelten: s+MU * w = Streckungsfaktor * u
L:=[u,v,w,x]:
| > | for k to 4 do LinearSolve(<MU|L[k]>,s);Strf[k]:=%[3];od: |
Die Streckungsfaktoren von u,v,w,x sind der Reihe nach:
| > | seq(Strf[k],k=1..4); |
![]()
Damit erhält man in der Ebenen E die affinen Punkte
| > | aH,bH,cH,dH:=seq(Strf[k]*L[k],k=1..4); |
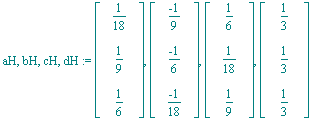
Probe (Ist aH-s in U ?):
| > | LinearSolve(MU,aH-s),LinearSolve(MU,bH-s),LinearSolve(MU,cH-s),LinearSolve(MU,dH-s); |
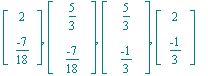
Liegt nun ein Parallelogramm vor ?
| > | Rank(<aH-bH|dH-cH>),Rank(<aH-dH|bH-cH>); |
![]()
Ja! Und das Parallelogramm ist nicht ausgeartet:
| > | Rank(<bH-aH|dH-aH>); |
![]()
Das Parallelogramm ist kein Quadrat, denn es gilt
| > | DotProduct(bH-aH,dH-aH,conjugate=false); |
![]()
| > |
| > |
(b)
Der wesentliche Gesichtspunkt bei (b) ist, dass die unendlich ferne Hyperebene in jeder der drei möglichen Konstellationen eindeutig ist. Die Verschiebung um s ist zwar dann willkürlich, solange s nicht aus H gewählt wird. Die Wahl eines anderen Vektors s' bedeutet für das Parallelogramm in H, dass es durch eine Streckung in ein Parallelogramm in H' überführt wird. Eine solche Transformation ist winkeltreu. Für die Entscheidung, ob ein Quadrat vorliegt oder nicht, ist die Wahl von s also unerheblich.
Wenn nichts besseres einfällt, muss man in den drei möglichen Fällen nun nur noch prüfen, ob das sich jeweils ja eindeutig ergebende Parallelogramm ein Quadrat ist oder nicht. Die Bezeichnungen von (a) werden weiterbenutzt.
In dem in (a) betrachteten Fall ergab sich kein Quadrat.
Wir rechnen die beiden verbleibenden Fälle
{a,b} und {c,d}, {a,c} und {b,d}
{a,c} und {b,d}, {a,d} und {b,c}
nun durch.
Dabei sind die meisten Zwischenergebnisse unterdrückt.
Vorbereitungen:
| > | restart: |
| > | with(LinearAlgebra): |
| > | u,v,w,x:=<1,2,3>,<2,3,1>,<3,1,2>,<1,1,1>; |
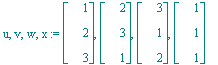
Im Fall
{a,b} und {c,d}, {a,c} und {b,d}
erhält man als Eckpunkte des Parallelogramms:
| > | S1:=op(IntersectionBasis([[u,v],[w,x]])): |
| > | S2:=op(IntersectionBasis([[u,w],[v,x]])): |
| > | MU:=<S1|S2>: |
| > | s:=<1,0,0>: |
L:=[u,v,w,x]:
| > | for k to 4 do LinearSolve(<MU|L[k]>,s);Strf[k]:=%[3];od: |
| > | seq(Strf[k],k=1..4): |
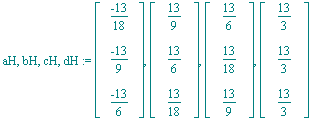
| > | aH,bH,cH,dH:=seq(Strf[k]*L[k],k=1..4); |
| > | Ctrl:=[Rank(<aH-bH|dH-cH>),Rank(<aH-cH|bH-dH>),Rank(<bH-aH|cH-aH>)]: |
| > | if Ctrl=[1,1,2] then print(`Es liegt ein echtes Parallelogramm vor!`); else print(`Fehler`); fi; |
![]()
Liegt ein Quadrat vor ?
| > | if DotProduct(bH-aH,cH-aH,conjugate=false)=0 then print(` ja!`); else print(`nein!`);fi; |
![]()
Im Fall
{a,c} und {b,d}, {a,d} und {b,c}
erhält man als Eckpunkte des Parallelogramms:
| > | S1:=op(IntersectionBasis([[u,w],[v,x]])): |
| > | S2:=op(IntersectionBasis([[u,x],[v,w]])): |
| > | MU:=<S1|S2>: |
| > | s:=<1,0,0>: |
L:=[u,v,w,x]:
| > | for k to 4 do LinearSolve(<MU|L[k]>,s);Strf[k]:=%[3];od: |
| > | seq(Strf[k],k=1..4): |
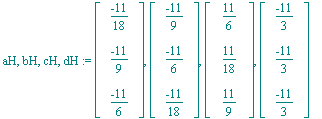
| > | aH,bH,cH,dH:=seq(Strf[k]*L[k],k=1..4); |
| > | Ctrl:=[Rank(<aH-cH|bH-dH>),Rank(<aH-cH|bH-dH>),Rank(<aH-dH|cH-aH>)]: |
| > | if Ctrl=[1,1,2] then print(`Es liegt ein echtes Parallelogramm vor!`); else print(`Fehler`); fi; |
![]()
Liegt ein Quadrat vor ?
| > | if DotProduct(bH-aH,cH-aH,conjugate=false)=0 then print(` ja!`); else print(`nein!`);fi; |
![]()
In keinem der Fälle ergab sich ein Quadrat. Es gibt also keine Hyperebene im
![]() derart, dass ein Quadrat entsteht.
derart, dass ein Quadrat entsteht.
| > |
| > |