Movies created in some pde2path demos


Home |Tutorials and Demos | Applications| Backlog

If bifurcation diagrams (BDs) become complicated (many branches, or long branches, and many bifurcations), then for presentations it may be useful to create movies illustrating the BD by moving a marker through the BD and plotting the associated solution. Moreover, Hopf orbits in 2D and 3D can often best be visualized by movies. Here we collect a number of movies generated in the demos. This proceeds by some ad-hoc scripts, and if you plan to make a movie, we suggest to copy the respective 'movie-demo-script' to your working directory and modify it there.
Remarks. a) These movies are generated from the data written to disk for creating figures. In particular, we generally write rather few points from the BD to disk (default p.file.smod=10), and hence have only few points with solution data available for the movies. If you want to create smoother movies, or do not care about disk space anyway, write more solution data to disk, e.g., set p.file.smod=1.
b) The movies are probably best viewed as full screen; you can also click pause and then drag the ruler to the the mvie frame by frame.
>
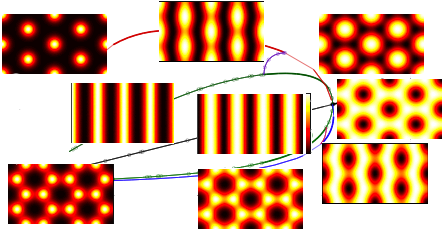
1D Allen-Cahn (AC) equation with imperfect bifurcations due to a nonhomogeneous Dirichlet BC at the right. See AC-tutorial. Two snaking branches of localized rolls in the 1D Swift-Hohenberg (quadratic-cubic) equation, see PF-tutorial (§3.2), and demos/pftut/sh/bdmov1D.m The 2D SH equation on a 'medium size' (quite small actually) domain see PF-tutorial (§3.8), and demos/pftut/sh/bdmov2D.m
The 3D SH equation on a long and slender bar, meant to illustrate localized 3D patterns, generated by initial guess; blue and red branch are BCCs and tubes, respectively; see PF-tutorial (§3.8), and demos/pftut/sh/bdmov3D.m A 'wandering boundary spot', meant to illustrate 3D mesh-adaption (slightly dragging behind the spot) by trullekrul. See Trullekrul-tutorial and demos/acsuite/ac3D/bdmovie3Dws.m. The 2D Schnakenberg RD system on a long and slender rectangle, illustrating 'beans' (orange) with bifurcations hexagons embedded in stripes; see PF-tutorial (§4.2), and demos/pftut/schnakpat/bdmov2D.m
The AC equation on a sphere, see PF-tutorial (§6.2), and demos/pftut/acS/bdmovacS.m. The Schnakenberg RD system on a torus, see demos/pftut/schnaktor/ and PF-tutorial (§6.4). The cubic quintic SH on a disk, here focussing on "daisy patterns", see here and /demos/JBDMV/sh35disk/
A four-armed snaking branch for SH35 on a disk, as one of the many further solution classes. For BDs with branches of periodic orbits (POs), we can create movies showing these at fixed parameter values. Here the complex Ginzburg-Landau (cGL) equation on a square, see hopfdemos/cgl/cmds2dsq.m (and sqmov.m). The cGL equation on a disk (O(2) symmetry), see Hopf tutorial (§6.2) and hopfdemos/cgldisk/cmds2d.m
The next 6 movies are from Geomtut. We start with mean curvature flow (MCF) from near a slightly unstable Enneper surface to the bifurcated surface with slightly lower area A, see demos/geomtut/enneper. Constant mean curvature (CMC) nodoids between two circles of radius 1 at distance 1; starting with a (stable) cylinder we obtain bifurcations to non-axisymmetric branches, see demos/geomtut/nodDBC/cmds1.m "Long nodoids", starting with a nodoid with one inner buckle, demos/geomtut/nodDBC/cmds2.m
Nodoids with periodic BCs in z, here on twice a minimal period cell, demos/geomtut/nodpBC/ Continuation of the Schwarz P triply periodic minimal surface in the period in z, demos/geomtut/TPS/cmds1.m CMC H ≠ 0 companions of Schwarz P, demos/geomtut/TPS/cmds2.m